ASD方程式、バブル、大陸、海、群島、フレアーホモロジー

バブル、大陸、海、島が、脳内で干渉して、混濁状態なので、整理してまとめます。抜粋は深谷さんの本からです。ドナルドソン不変量の計算局面は未対応

ASD方程式

リーマン幾何学では、ある計量（metric）に対するレヴィ(Levi)=チビタ(Civet)接続(connection)の曲率(curvature)を考えますが、ここでは、\(\zeta_k\)の\(SU(2)\)接続全体の作る空間\(\mathcal{A}(M,\zeta_k)\)をとし、これをゲージ変換群(gauge transformation group)で割った商空間\(\mathcal{B}(M,\zeta_k)=\mathcal{A}(M,\zeta_k)/\mathcal{G}(M,\zeta_k)\)を考えます。接続\(A\)のゲージ群の作用による軌道、同値類を\([A]\in \mathcal{B}(M,\zeta_k)\)と書きます。

\(SU(2)\)のLie環\(su(2)\)上の共役表現(adjoint representation)を用いて\(\zeta_k\)からベクトル束\(E=Ad \zeta_k\)を得ます。E値二次微分形式、つまり、このベクトル束と\(\Lambda^2 (M)\)とのテンソル積\(E \otimes \Lambda^2 (M)\)を考えます。このとき、

$$\Gamma(E \otimes \Lambda_{+}^2 (M)) = \{u \in \Gamma(E \otimes \Lambda^2 (M)) | \mathord\ast u = u\}$$

と定め、ベクトル束\(\mathcal{A}(M,\zeta_k)\times_{\mathcal{G}(M,\zeta_k)}\Gamma(E \otimes \Lambda_{+}^2 (M))\to\mathcal{B}(M,\zeta_k)\to\)の切断(section)\(A \mapsto F_A^{+}= F_A + \mathord\ast F_A\)をとり、その0の逆像を、

$$\mathcal{M}(M,\zeta_k)=\{[A]\in \mathcal{B}(M,\zeta_k)| F_A^{+} =0\}$$

とおきます。多様体\(M\)のドナルドソン不変量とは\(\mathcal{M}(M,\zeta_k)\)の表すホモロジー類(\(H_*(\mathcal{B}(M,\zeta_k);\mathbf{Z})\)の元)です。

そして方程式\(F_A + \mathord\ast F_A=0\)の解である接続のことを反自己双対接続(anti-self-dual connection)と呼びます。省略してASD接続とも呼ばれます。

鬼ややこしいから冥土いきしそうだ

ホッジ(Hodge)作用素によって、双子のペア赫あかとBL

$${\color{blue}{BL}}\overset{\mathord\ast}{\leftrightarrow}{\color{red}赫}$$

本書ではこれに関する複雑な議論に巻き込まれることを好まないので、簡単に次の定義の

み与えることにする。

アルプスパープルという品種のアジサイの色、淡紫たんし。漢字を、一番使われている「紫」でなくて、古い字の「茈むらさき」にしようか迷いました。コスモスやラベンダーの花も大好きです。アメジストもジュエリーだが紫です。人々をperplex(当惑させる)

$${\color{purple}{淡紫}} = {\color{red}赫} + {\color{blue}{BL}}$$

意図的に消し去られたので\({\color{purple}{淡紫}}=0\)になる。

、サンキュー、双子を足し算、和を調べて、ゼロ、色も全く無い、透明、華麗にフェイドアウト

フレアーホモロジー

黄色いヘリポクターがはるか上空を飛んでいる。上から目線でどんな絵画を描けるのでしょうか。

窓の外からイヌの鳴き声が聞こえます。米田の補題

米田埋め込み(Yoneda embedding)

かわってない

わからねー

何故だ

脱線してました。。気分的に、3次元多様体が対象で4次元多様体が射の圏があって、境界の貼り合わせが、射の合成。フレアーホモロジーの集合への関手がドナルドソン不変量

米田写像（Yoneda map）と呼ばれる全単射

情報は、ぜんぶidで得られる

青いセーター、集まるターン？

Hom関手

リンク

米田の補題を1枚の図式で描こう

zenn.dev

前節で述べたようにフレアーホモロジーとは３次元多様体の上の接続全体のゲージ同値類の空間\(\mathcal{B}(M,\xi)\)上の\(\infty /2\)次元のホモロジー群であった。これを定義するためにモース理論を用いる。

したがってヤン-ミルズ汎函数をモース関数として使って得られるのは、有限次のホモロジー群すなわち\(\mathcal{B}(M,\xi)\)の普通のホモロジー群である。

W%tten複体

フレアーサイクル

そこでここでは別の汎函数すなわちチャーン(Chern)-サイモンズ(Simons)汎函数を用いる。

大陸、海、島

\(X\)を完備で向きの付いた４次元多様体で、\(X-K\)(\(K\)はコンパクト集合)は\(M \times (0,\infty)\)と等長的とする。

\(K\)は大陸で、\(M\)は海岸線、美しい波が寄せては返す浜辺を想像しています。海岸線から無限に延長される海が\(M \times (0,\infty)\)。

\(A_l\)の\(M \times [-T_l,T_l] \subseteq X(T_l)\)への制限をかんが,輪切りにして、\(2T_l\)個の\(M \times [-1,1]\)に分けます。

マクロな世界の上にASD接続

ほとんど平坦な接続

曲率のノルムが十分小さければ、平坦接続で近似できる。

二つのASD接続をはり合わせます。二つのASD接続を足す

平たく言えば\(Pat_0 (T)\)を少し動かして\(\mathcal{M}(X(T),\zeta_{k_1+k_2})\)への写像に変形できることを言っている。

此方岸と彼岸がはさむ川のよう

川を積み重ね、シマシマのウデにして、コントラスト

般若のシンワンノジュツ

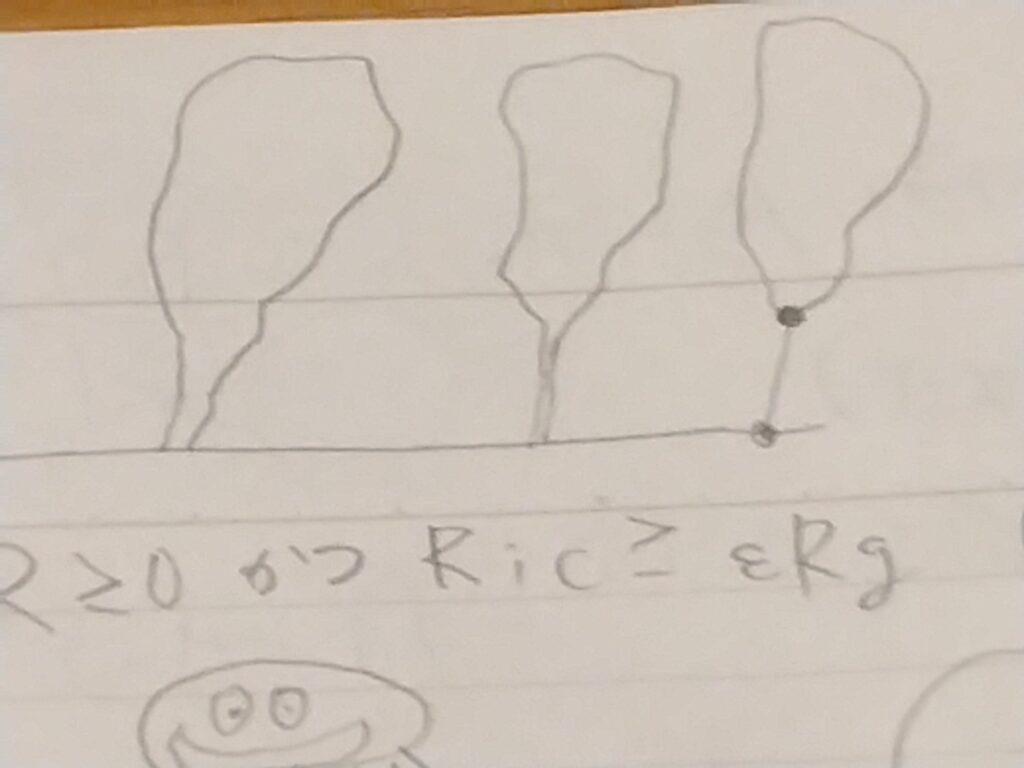
バブルと呼ばれる現象とはな

ミクロなツブツブがあって、そこから髪の毛みたいな細い糸

お米炊けたら、背フルで食べてくれるー３０分くらいで、

アツアツスープのとんこつラーメンにペッパーをかけて

海岸線のボリュームをちっちゃくしていって、すると、海が、配管（pipe）みたいに、ラーメンみたいに、髪の毛みたいになり、ガリガリになり、finishでは、ちぎれた大陸とツブツブになった海岸線だけが、残ります。

家の各部屋にキッチンがあって、それぞれのキッチンが泡まみれ

もう無理かも・・・・・・なんということでしょう

泡沫

集合\(\mathcal{CM}(M,\zeta_k)\)を

$$\mathcal{CM}(M,\zeta_k)=\bigcup_{k \ge l}\mathcal{M}(M,\zeta_l) \times S^{k-l}(M)$$

で定義する。

４次元多様体上の\(SU(2)\)を構造群にもつベクトル束は第２チャーン数、物理ではインスタントン数で完全に定まる。インスタントン数とは、ASD接続のエネルギーみたいなものと考えて、いいんですかね？

\(A_i\)たちはASD接続であるからその曲率の\(L^2\)ノルムはチャーン(Chern)数の定数倍で、したがって\(i\)によらない。

バブルでインスタントン数を損します。なんでなんでなんで？

$$\dim \mathcal{M}(X,\zeta_k;a)=8k+3(b_1(X)-1-b_2^{+} (X))-\eta(a)$$

次元を損するってなんですか？

4次元えんばん\(D^4\)

ウーレンベック

離島を調査だニャー

ふらふらと酔歩、ランダムウォークして

あればいいんだけど、ないならないで

零

鳴門の渦潮

モース、交叉形式、

可約接続の扱い、これが相対ドナルドソン不変量の定義にはいろいろ悪さをする

フリードマン-モーガンの爆発公式

楕円型指数の和公式、スペクトル流(spectral flow)

２つの多様体を長いチューブで繋げる話で、多様体が大陸、長いチューブの部分が海と海に浮かぶ島。島があると、どうなるのでしょうか。キッチンのシンクで水の流れが悪くなる？

モース指数(ヘッセ行列の負の固有値の個数)\(\eta\)に段差がある、ということです。

（可約接続を無視して）

ちょっとしんどいかな

よって\(\)すなわち大陸から離れたところには島はない。また\(\)すなわちバブルは生じていない。

指数定理

次元の計算すなわちAHS複体の指数も調べなければならない

これはどちらかというと技術的な問題なのだが、いろいろなところで現れるデリケートな問題で、粗く考えていてどこか変になるのは横断正則性が絡む場合が多い。

つまり摂動によって、細かい例外をムシすれば、

\(E \otimes \Lambda^0 (M) \stackrel{d_A}{\to} E \otimes \Lambda^1 (M) \stackrel{d_A^{+}}{\to} E \otimes \Lambda_{+}^2 (M) \)

AHS複体の第２コホモロジーが0でなければならかった

ということです。

頭痛が。そんなことある？ばんくおぶ

も樹雷

入ります

だけでは未完了

ないないないない

時期尚早

部分的には

SW

領域展開。シジミチョウが飛んだ。警告か。

おしゃべり：私は数学の発展は一般化とそれに続く特殊化によってなされると信じている。我々は鷲のように飛び上がり獲物をめがけて舞い降りるべきである。\(X(3,6)\)の一意化物語のためには、少なくともバッタ程度には飛び上がらなければならない。

バッタ、息してる？長くなりそうです。